AFRL MSTC-UM RPI Collaborative Center in Aerospace Vehicle Design (CCAVD)

Air Force Research Laboratory

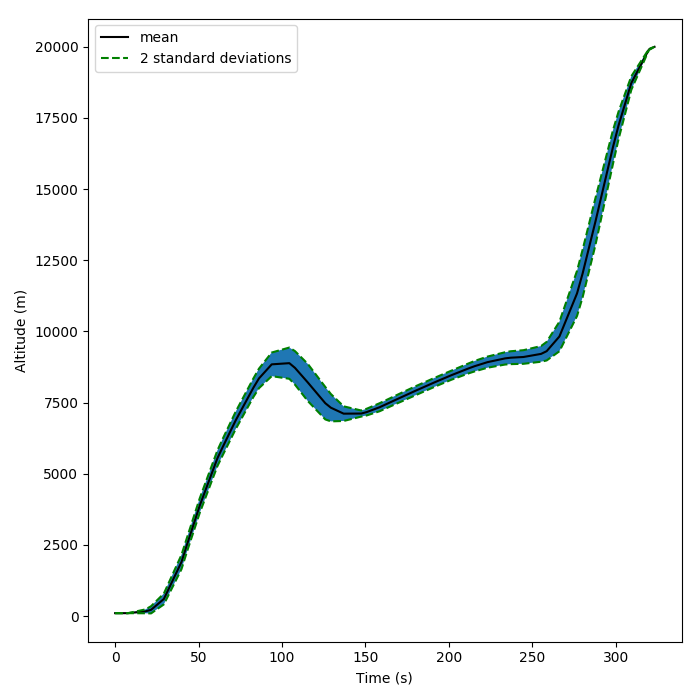
A robust design is one that is less sensitive to uncertainty than alternative designs. For example, a robust hypersonic engine is relatively insensitive to variations in the inlet velocity, temperature, and pressure. In optimization under uncertainty (OUU), robustness is typically achieved using a composite objective involving the mean and variance of the figure of merit. The difficulty in high-fidelity OUU is that the mean and variance are high-dimensional integrals with computationally expensive integrands. This motivates the need for dimension reduction in the uncertain, or stochastic, parameter space, as well as efficient surrogates to model the high-fidelity models. In this task for the AFRL CCAVD, we will use Arnoldi’s method to estimate the dominant eigenvectors of the integrands’ Hessians, and then sample in this reduced space using Monte-Carlo simulation or stochastic collocation.

Simulation-Enhanced Virtual Design Environments for Fluid Systems (CAREER Award)

The National Science Foundation

Fluid systems, such as aircraft, biomedical pumps, or turbines, play a vital role in many sectors of the U.S. economy. Due to the complex physics of fluid flow, these systems are often difficult and costly to design. This presents a barrier to start-up companies seeking to develop products that involve such complex fluid flows. The complicated nature of fluid flows also poses a barrier in engineering education, where students often struggle to achieve intuition regarding fluid flows. To mitigate these barriers, this award envisions an immersive, virtual-reality design environment in which engineers can interact with aircraft or heart pumps in the same way artists interact with clay. A key requirement of this vision is the ability to provide engineers with instantaneous performance predictions as they shape their virtual designs. This award will help build the knowledge necessary for real-time prediction of complex fluid flows, thereby enabling the next generation of tools for immersive computer-aided design and engineering education.

Optimization of Complex Systems using Imperfect Data from Large-scale Simulations

Air Force Office of Scientific Research

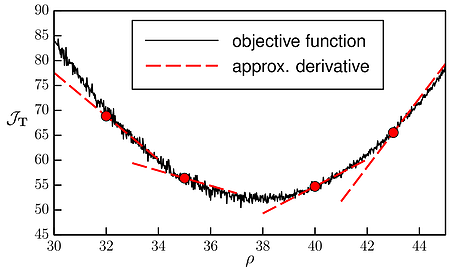
The objective of this project is to create an optimization framework that can use “imperfect” data to design complex high-dimensional systems. The target applications share three properties: 1) accurate predictions require computationally costly simulations (e.g. unsteady turbulent flows); 2) the design space is high dimensional, and; 3) the quantities of interest and their gradients have errors that cannot be eliminated in practice.

Scalable Multifidelity Design Optimization: Next Generation Aircraft and their Impact on the Air Transportation System

National Aeronautics and Space Administration

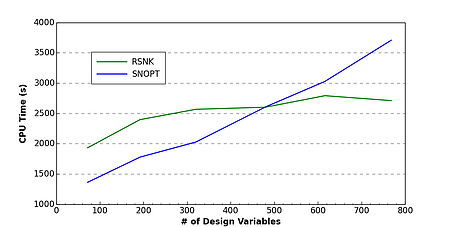
This is a multi-university effort led by the MDO Lab at the University of Michigan. The project has several objectives, but the Optimal Design Lab’s focus is on creating scalable optimization algorithms that are well-suited to reduced-space PDE-constrained optimization.

Enabling Multidisciplinary Design Optimization: Inexact-Newton-Krylov and the Individual-Discipline-Feasible Formulation

The National Science Foundation

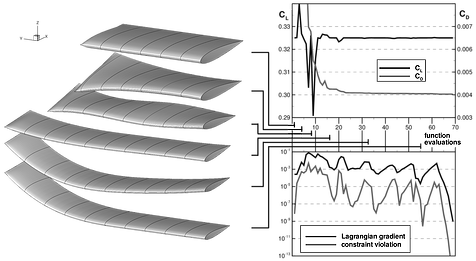
This project is investigating matrix-free Newton-Krylov algorithms as a means of solving multidisciplinary design optimization problems. More precisely, we are exploring the use of matrix-free algorithms to solve simulation-based design optimization problems in a modular way. Modularity is attractive for these problems because many legacy software libraries already exist that can analyze and optimize problems involving a single discipline, for example fluid dynamics. In contrast, few libraries are available that can analyze complex multidisciplinary systems, let alone optimize them. To achieve a modular approach, we have adopted the so-called individual-discipline-feasible (IDF) formulation. Historically, the IDF formulation has been limited by the need to form computationally expensive matrices demanded by conventional optimization algorithms. This motivates our investigation of Newton-Krylov algorithms, which will enable a scalable and matrix-free implementation of IDF.